Ethereum MPT (Merkle Patricia Tries) Deep Dive

Introduction

Recently, I’ve been working on a fascinating project that involved migrating a smart contract’s state tree data structure from Red-Black Trees to Trie structures. This experience gave me deep insights into how Ethereum manages state data and the elegant engineering decisions behind the Modified Merkle Patricia Trie (MPT). As a programmer with over 10 years of experience, I want to share my understanding of these data structures and their performance characteristics in blockchain applications.

Data Structures Overview

Red-Black Tree

Red-Black Trees are approximately balanced binary search trees containing red and black nodes, ensuring that the height difference between left and right subtrees of any node is less than double.

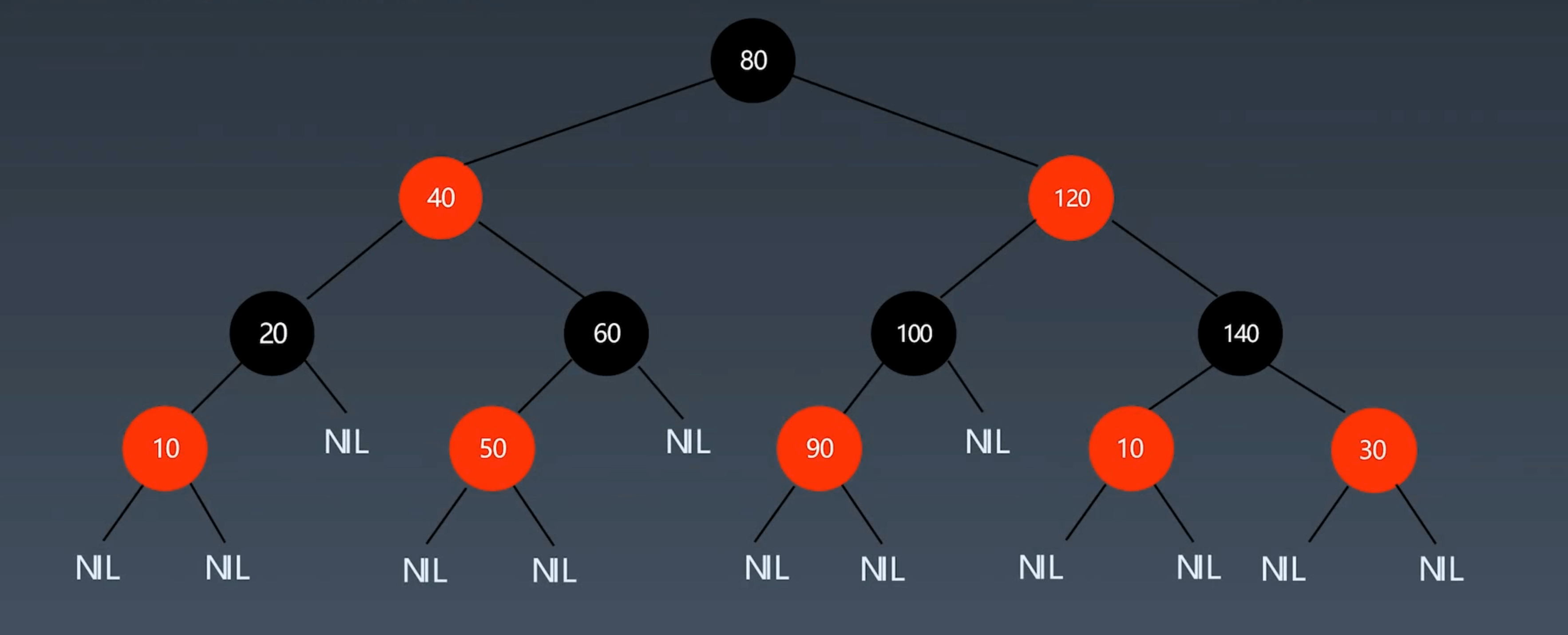
Properties

A Red-Black Tree must satisfy these five properties:

1. Each node is either red or black
2. The root node is black
3. All leaf nodes (NIL) are black
4. Both children of every red node are black
5. Every path from any node to each of its leaf nodes contains the same number of black nodes

Red-Black Trees aren’t perfectly balanced but maintain black-height balance, meaning left and right subtrees have equal black node depths. This approximate balancing reduces rotation frequency, lowering maintenance costs while maintaining O(log n) time complexity.

Operations

Red-Black Trees maintain self-balance through three primary operations:

• Left Rotation
• Right Rotation
• Color Changes

Red-Black Tree vs AVL Tree Comparison

• AVL Trees: Provide faster search operations (due to perfect balance)
• Red-Black Trees: Offer faster insertion and deletion operations
• Storage: AVL trees store more node information (balance factors and heights), requiring more memory
• Use Cases: AVL trees are preferred for read-heavy operations (databases), while Red-Black trees excel in write-heavy scenarios (language libraries like map, set)

Trie (Prefix Tree)

Tries, also known as prefix trees or digital trees, are commonly used for statistical analysis and sorting large string collections, such as text indexing in search engines.

They minimize unnecessary string comparisons, providing efficient query performance.

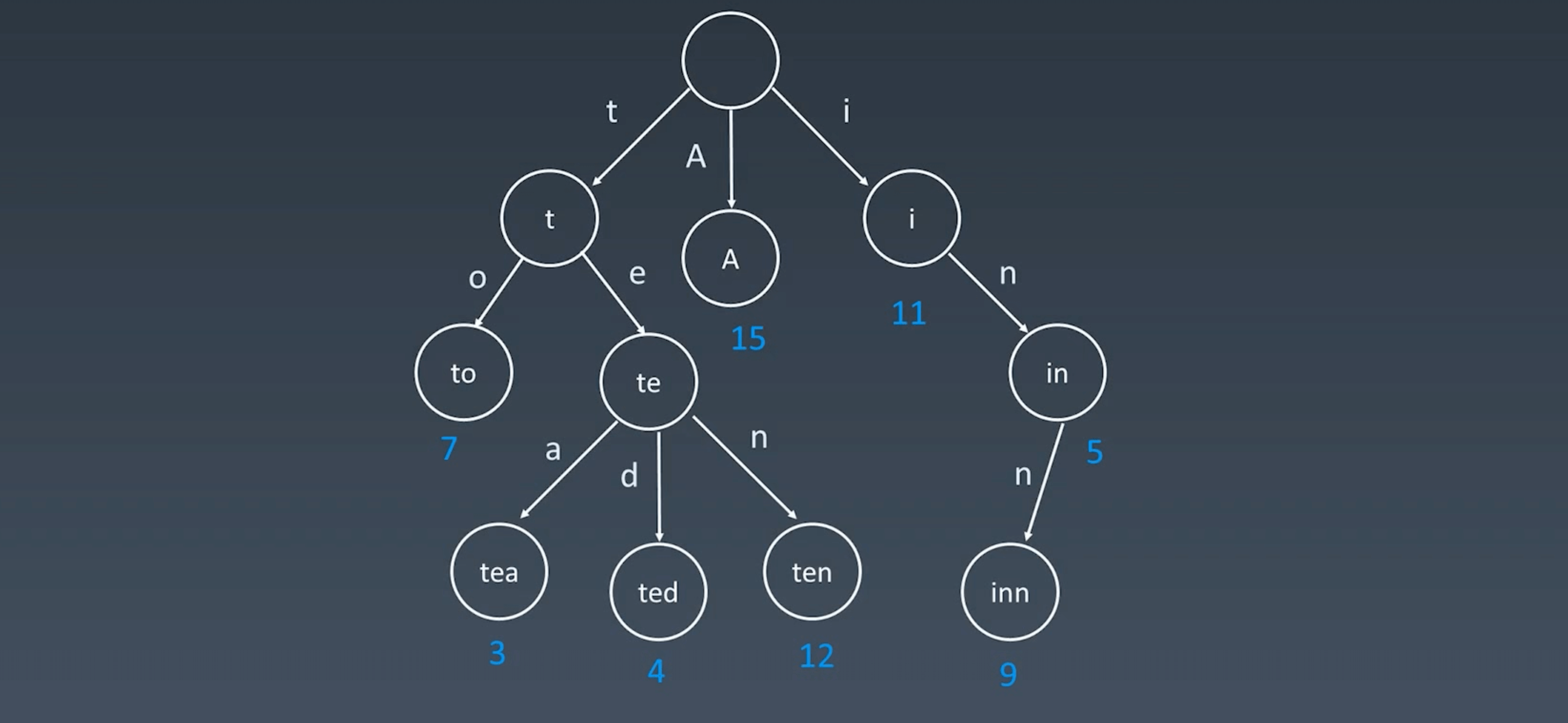
Properties

1. Nodes don’t store complete words
2. The path from root to any node represents the string associated with that node
3. All children of a node have path characters that are different
4. Nodes can store additional information like word frequency

Internal Node Implementation

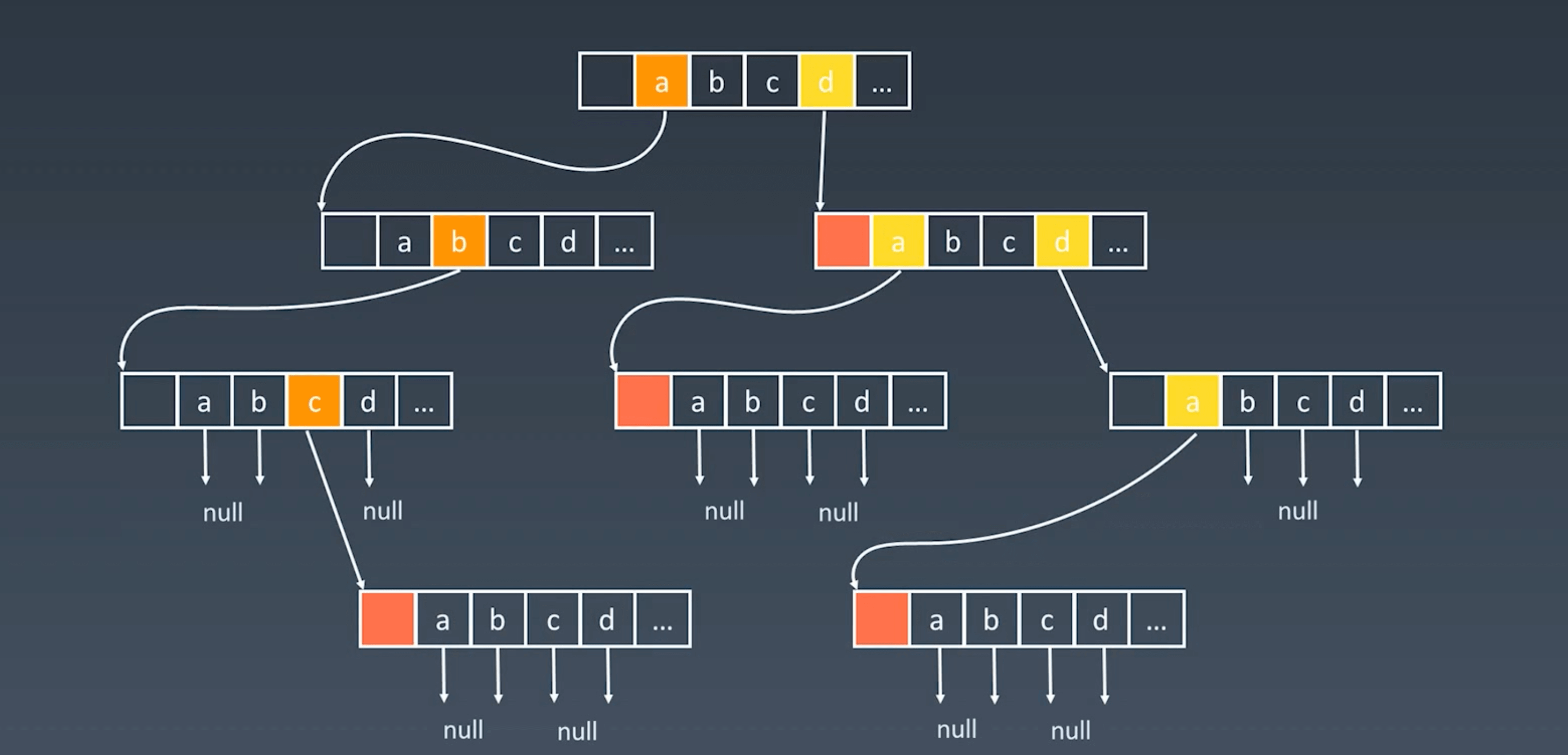
Tries have relatively low height but consume more storage space. The core philosophy is trading space for time efficiency.

By leveraging common prefixes of strings, Tries reduce query time overhead and naturally solve problems like word suggestion systems.

Code Implementation

class Trie {
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }

    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }

    public boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    private Trie searchPrefix(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            char ch = prefix.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                return null;
            }
            node = node.children[index];
        }
        return node;
    }
}

Modified Merkle Patricia Tries

Ethereum Account State Storage Challenges

Traditional approaches face several issues:

1. Hash Table Storage: Using Key-Value hash tables means every block generation requires rebuilding the entire Merkle tree, even when only a small percentage of accounts change - highly inefficient
2. Direct Merkle Tree: Standard Merkle trees lack efficient search and update methods
3. Sorted Merkle Tree: Impractical because new Ethereum account addresses are randomly generated, requiring constant resorting upon insertion

MPT Structure Benefits

Ethereum’s MPT leverages Trie structure advantages:

1. Order Independence: Trie structure remains unchanged regardless of insertion order, naturally sorted even with new value insertions - perfect for Ethereum’s account-based architecture
2. Excellent Update Locality: Updates don’t require traversing the entire tree

However, standard Trie structures waste significant storage space and perform poorly with sparse key-value distributions. Ethereum account addresses are 40-character hexadecimal numbers (approximately 2^160 possible addresses), creating extremely sparse distribution (intentionally designed to prevent hash collisions).

Therefore, Trie structures require path compression, creating Patricia Tries. After compression, tree height significantly decreases, improving both space efficiency and performance.

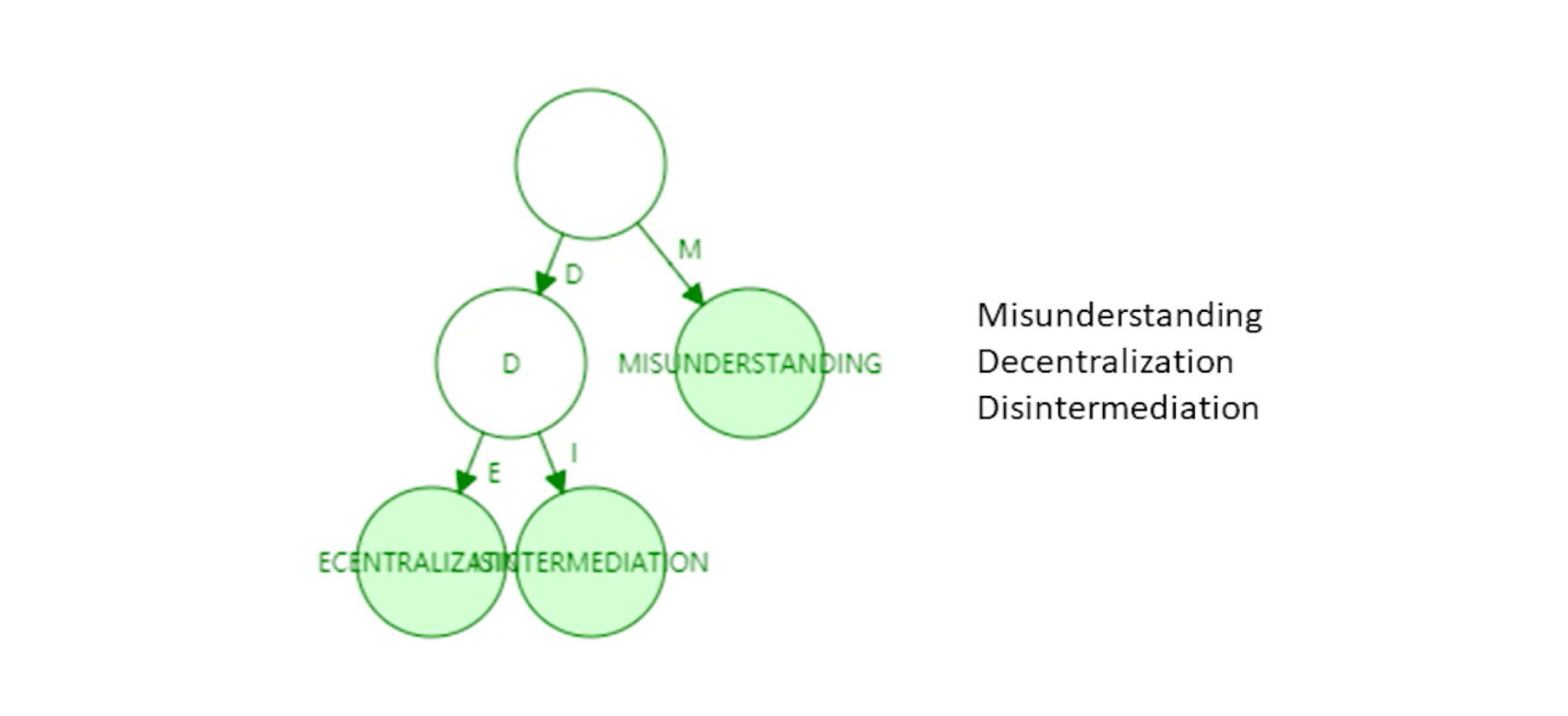
Modified MPT Structure

Ethereum actually implements a Modified MPT structure:

When publishing new blocks, state tree node values change not by modifying existing values, but by creating new branches while preserving original states (enabling rollback functionality).

In Ethereum, forks are normal occurrences. Orphaned block data must roll back, and since Ethereum supports smart contracts, maintaining previous states is essential for smart contract rollback operations.

Performance Analysis

Through my implementation experience, I found that:

Red-Black Trees excel in:

• Predictable performance with O(log n) guarantees
• Memory efficiency for sparse data
• General-purpose key-value operations

Modified MPT excels in:

• Cryptographic verification (Merkle proofs)
• State rollback capabilities
• Efficient bulk updates affecting related keys
• Blockchain-specific requirements

The choice between these structures depends heavily on your specific use case. For blockchain applications requiring cryptographic proofs and state history, MPT is superior. For general applications requiring balanced performance, Red-Black Trees remain excellent choices.

Summary

This analysis covers Ethereum’s MPT data structure compared to Red-Black Trees. During my years of development, I often wondered if complex data structure knowledge learned in academic settings would have practical applications. This project proved that fundamental computer science concepts remain crucial in cutting-edge technologies like blockchain.

Understanding these data structures deeply has made me appreciate the elegant engineering decisions in Ethereum’s architecture. The MPT represents a perfect marriage of cryptographic security, performance optimization, and blockchain-specific requirements.